正三角形公式的相關文章
正三角形公式的相關公司資訊
正三角形公式的相關商品
オイラーの多面体公式から証明される定理
瀏覽:664
日期:2025-12-11
3次元凸多面体の頂点,辺,面の数をそれぞれv,e,fとすると, v-e+f=2 (オイラーの多面体定理) が成り立ちます.たとえば,正八面体ではf=8,v=6,e=12.切頂20面体ではf=32(正五角形12枚,正六角形20 ......看更多




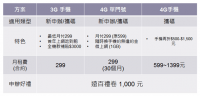
![[科科買東西] 4G 上網 299 元搞定?遠傳網路門市在家申辦,輕鬆激省一大筆](https://www.iarticlesnet.com/pub/img/article/70943/1446794470308_s.jpg)





![[經典遊戲] - 飛行棋大戰 Battle Ludo v1.4 大更新](https://www.iarticlesnet.com/pub/img/article/19651/1403907114549_xs.jpg)
![[11 12] iPhone iPad 限時免費及減價 Apps 精選推介](https://www.iarticlesnet.com/pub/img/article/4468/1403803666806_xs.jpg)
![[10 12] iPhone iPad 限時免費及減價 Apps 精選推介](https://www.iarticlesnet.com/pub/img/article/4498/1403803843393_xs.jpg)
![[9 12] iPhone iPad 限時免費及減價 Apps 精選推介 2](https://www.iarticlesnet.com/pub/img/article/4523/1403804017984_xs.jpg)
![[6 12] iPhone iPad 限時免費及減價 Apps 精選推介 2](https://www.iarticlesnet.com/pub/img/article/4577/1403804436227_xs.jpg)
![[9 12] iPhone iPad 限時免費及減價 Apps 精選推介 1](https://www.iarticlesnet.com/pub/img/article/4529/1403804119747_xs.jpg)







